Ex84 计算模型的注意事项
上一节我们简单介绍了一下搬砖的原则性问题。这一节,我们主要分析下搬什么砖的问题。继续采用甲醇在金属表面上分解的这个例子。物化书中我们学过表面反应的基本步骤: 1)反应物分子的吸附;2)表面反应; 3) 产物脱附。
甲醇分解反应第一步是先从气相吸附到催化剂金属表面。 对于这一步, 我们自然需要从甲醇的气相分子出发,研究甲醇分子在表面上的吸附结构。其中涉及到一些基本的计算细节:
1) 如何优化气相分子的结构,计算频率呢?
2)如何优化体相结构,切面,优化,计算表面相关性质:比如表面能、功函数等。
这些我们前面也已经讲过了,所以直接跳过。
这里还有一个问题在于,你去用什么表面去模拟催化剂? 比如说Cu,可以有(111), (110), (100), (211)….等各种不同的指数面,你选哪个来算?为什么选这个来算?这涉及到:我们的研究对象是什么?通过研究这一对象,我们要解释什么?期望获得什么样的结果?对于催化反应来说,我们的研究对象有2个:催化剂和它所催化的反应。
如何获得催化剂的合理模型就是一个至关重要的问题了。一般来说,有下面几个供大家参考的办法:
1)选稳定的表面,也就是表面能低的那个,对于纳米颗粒来说,尺寸如果够大,那么表面能低的表面原子在所有暴露的表面原子中的比例会高,那么可以近似用这个面来模拟催化剂的情况;那么尺寸多大才算足够大呢?
我们可以尝试着从两个极端来进行思考:我们的催化剂如果是金属的话,如果采用一个单金属原子作为催化剂模型,可以想象吸附能肯定很大。当原子慢慢堆积成团簇,团簇再慢慢长到无穷大的时候,吸附能也随之发生变化。我们取无穷大时(最稳定的表面)的吸附能(E0)作为参考,看看金属团簇多大尺寸的时候,吸附能跟E0接近。那么该尺寸以及更大的纳米颗粒就可以用无穷大的催化剂模型来模拟,也就是最稳定的表面。一般来说,纳米颗粒的直径大于2nm(胆儿肥的)的时候,可以用最稳定的表面来模拟催化剂。保守些,直径大约3nm的时候可以放心地去用,不会有什么问题。
下面推荐一本书: Fundamental Concepts in Heterogeneous Catalysis 。书中第21页, 作者用O在Pt(111)表面的吸附能作为参考,测试了不同纳米颗粒尺寸时的吸附能,发现直径在2nm的时候,已经非常接近了。前面说的那个2nm,也是从这里来的。如果你想问我这本书从哪里可以下载,可以关注公众号:BigBroScience,然后回复:ex84 。
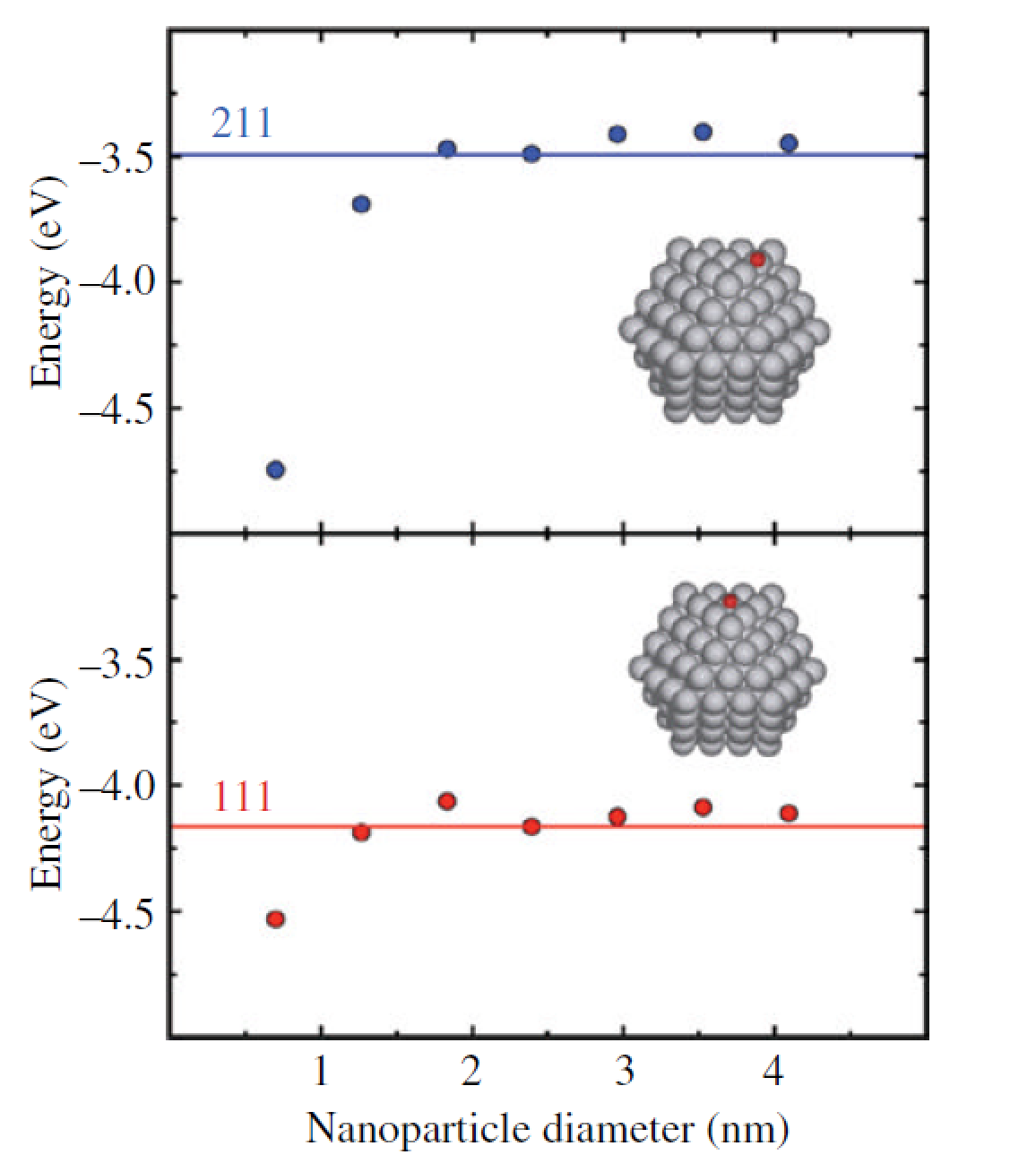
2)对于前面的一番说法, 也会有人说,催化剂的活性位不一定在平坦的表面上,边边角角,台阶上可能更容易发生反应。如果你单纯把工作聚集在最稳定的表面上,肯定会遗漏些什么?这也是很多审稿人喜欢折腾我们这些小白鼠的地方。一个金属有很多不同的指数面,单纯考虑最稳定的是一个保险折中的办法。因为不管你的体系搞的再复杂,跟真实情况相比,模型终究是简单的。我们只是尽自己可能去尝试着理解,解释实验的现象,描述下体系的性质,以及进行一些比较简单直接的预测。但是,如果你要深究这些,兴趣也恰好落在在这一块,那么可以对体系的各个相关结构进行一个全面的计算,分析不同表面结构,性质,反应活性有什么不同。在这个全面的计算体系中,
除了各种台阶面,最稳定的表面你还是要算的,这样才能有个对比。原则上说,只要你力气足够,资源充足,可以选任何你想要的表面来计算;但问题是你总会有吐的时候,如果想多算几个面的时候,要留意下面的几点:
注意-1:开放的表面在计算表面能,slab优化或者吸附的时候,层数的影响会很大,这个前期的测试工作要做好;
注意-2:生存法则:
A)灌水第一条:同一个反应, 这个指数面算一下发一篇文章,换个面再发篇文章,再换个面继续发文章….
B)灌水第二条:同一个面: 算一个反应发一篇文章,换个反应算一下再发一篇文章,再换反应;
C)灌水第三条:反应,表面和反应交替,排列组合式发文章。
3)还有一种情况,就是我们手上有实验数据,想模拟一下实验的结果。这个时候,就可以参考下催化剂的表征结果,有针对性地选取催化剂的模型,使其尽可能地去描述催化剂的结构。
注意的有以下几点:
A) 如果做实验的人找你帮忙算个东西,能推掉就推掉,别在上头浪费自己的功夫,顶死也就是个共同一作,国内基本不认可,做无用功;如果刚开始推不掉,就看看他的实验表征结果,一般般的表征以模型搭不出来为由直接拒掉;好的模型是成功的重要因素。前面我们说了,模型再复杂也是简单的。再考虑到实验表征的结果不确定性,你有很大的几率是跟实验上对不上的,到头还是白忙活。很多人会拿工作要冲子刊,杰克斯,俺狗娃为由诱惑你上船,要掂掂自己的分量,别头脑发热用屁股做决定。
B) 对于做实验的人来说,99%会低估计算的复杂性,总以为鼠标点点就OK的事情,其中也不乏一些所谓的大牛们。话虽然难听,却也是大实话:不要瞎几把评论自己不懂的领域。真想找人算一下,要找个靠谱的合作伙伴,找到不靠谱的瞎算,投文章更会给整个工作拉分。
4)最后一个及其重要的就是,认真进行文献调研。看看前人都是怎么选取的,为什么这样选?根据什么依据来选?最终确定自己的计算模型。
关于模型的一些就先到这儿, 本篇的工作主要是重复一遍前人已经算烂的反应,然后在此基础上,分析BEP和TSS线性关系。就直接拿各个金属最稳定的表面来计算了。那么, 什么是BEP线性关系? 这里的BEP的全称是:Bell–Evans–Polanyi principle. 指的是对于同一类型的N个反应,这些反应的能垒和反应热之间存在的一个线性关系: $E_a$= $\alpha \Delta E$ + $\beta$ 。更详细点的介绍,参考维基百科搜索:Bell–Evans–Polanyi principle。起初这个关系是基于均相反应来说的。在2000年的时候,Neurock将这个关系引入多相催化体系,发现表面反应也存在这一关系。随后,经过了Norskov等人的继续研究,相关的文章就越来越多了。有兴趣的可以通过下面的几篇经典文献开始接触,然后再逐渐深入:J. Catal. 191, 301 (2000), J. Catal. 197, 229 (2001), J. Chem. Phys. 114, 8244 (2001)
BEP关系有啥用呢?主要有两点:
关键的一点就是用来节约机时:过渡态不是一个稳定的结构,它的优化需要的计算时间比直接优化反应物种的要多得多。插8个点,也就是8倍的单个优化。再加上计算还经常容易失败。因此我们可以通过BEP关系,跳过TS的优化,直接预测反应的能垒,从而达到节约机时和生命的作用。这个方法简单粗暴,与直接进行反应路径扫描相比,在时间成本上具有压倒性的优势,但精度和准确度上就会稍逊一筹。
另外一点是来预测反应的能垒,这个其实和上面的有些重复,但角度不同。比如一个复杂的催化体系,基元反应数目成千上万,我们挨个算过渡态显然不可行。但是中间体的数目明显少的多,那么我们通过中间体获取反应热之后,通过BEP关系得到反应能垒,也就有了动力学的一些基本数据,从此出发,可以做一些机器学习以及微观反应动力学的模拟工作。从而跨越理论计算的原子分子尺度来到达一个更为宏观的尺寸和时间的尺度,也就是所谓的多尺度模拟。
继续前面的分析,如果中间体的数目也很多,算都算不完,那该怎么办?这个也可以通过一些线性组合,数据分析的方法来进行预测。比如通过Group Additivity的方法,可以将对分子中不同group的能量的求和来获得。具体的内容在后面其他章节再慢慢进行介绍。由于篇幅关系,本节(ex84的上半部分)主要是让大家对自己的研究对象有一个明确的认识,为什么研究它?为什么不研究别的?下半部分介绍中间体计算的一些注意事项。